2.1 Curve Sketching

Definitions

critical point

A point where the first derivative is zero.

local minimum

A point where the first derivative is zero, and the second derivative is positive on both sides. 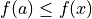f(a) \le f(x) for all points within a certain region if the minimum is at a.

local maximum

A point where the first derivative is zero, and the second derivative is negative on both sides. 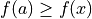f(a) \ge f(x) for all points within a certain region if the maximum is at a.

absolute maximum/minimum

The minimum or maximum for all the points in the range.

extreme point

A local minimum or a maximum.

point of inflection

A point where the second derivative changes sign. This can occur where the second derivative is undefined or zero.

even function

f(-x) = f(x)

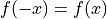
odd function

f(-x) = -f(x)

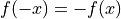
Curve Sketching Process

Step 1

Identify where 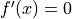f'(x)=0 (Critical points.) The tangent line is zero here.

Step 2

Where 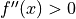f''(x)>0, it is concave upward. Where 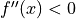f''(x)<0, it concave downward.

Step 3

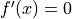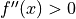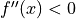Where f'(x)=0, If f''(x)>0, then it is a local minimum point. If f''(x)<0, then it is a local maximum point.

Step 4

If 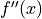f''(x) changes sign (at zero or undefined points) it is a point of inflection.

Step 5

Even and odd functions need only be investigated for positive x. Flip or rotate it when done.